Electronic Measurement

  1. Home
  2. Electronic Measurement of Semiconductor Quantum Dot Devices

Figure 1 (a) Rabi oscillation. Inset: Oscillation quality factor as a function of rf amplitude. The red symbol marks the condition for the maximum quality factor. (b) Representative Rabi oscillation with visibility higher than 97%. The oscillation is fit to the sinusoidal function with the Gaussian envelope. (c) Singlet return probability as a function of the number of random Clifford gates obtained from a single qubit standard and interleaved randomized benchmarking. Traces are offset by 0.3 for clarity. (d) Density matrices (top row) and Pauli transfer matrices (bottom row) evaluated by gate set tomography.

Figure 2 (a,b) The exchange oscillations of QL (QR) depending on the state of the other qubit as control. The lower and upper traces are measured when the state of QT is singlet and triplet, respectively. (c) The simulated maximum attainable Bell state fidelity as a function of JL for bilinear (black) and superlinear (red) JRL. The fidelity is estimated at JR = 500 MHz. (d) The estimated maximum attainable Bell state fidelity from the experimental values. The fidelity shows an increasing tendency with a maximum value of ~0.95. The error bars are estimated from the uncertainty of JRL and Techo of each qubit.

Figure 3 (a) Schematic diagram of pulse sequence for a Ramsey oscillation, the z-axis manipulation on Bloch sphere during the free evolution time tevol and the pulse amplitude Vevol. π/2 pulse was applied with Vevol = 0.27 V and properly calibrated pulse duration time. (b) The representative Ramsey oscillation with the probability of triplet state PT in Bz,ext = 400 mT and Vevol = 770 mV, which shows high coherence time T2* and quality factor Q* values. The left and the right figures were 10000 and 100 times averaged, respectively. (c) Ramsey oscillations as a function of tevol and Vevol. The white dashed line indicates the contour line of T2* extracted from each Ramsey oscillation line of Vevol. The inset shows the reproduced Ramsey oscillation results through numerical simulation. (d) Line-to-line FFT result of (c). The expected transition line of the right dot is indicated as a dotted line on the right figure. Two dashed orange lines show the linearly fitted fQ with Vevol before and after the frequency shift of ΔfQ ~ 1.7 MHz during the charge transition of QDR. A small bump with maximum ΔfQ ~ 0.4 MHz, indicated by the red dotted line, is the footprint of the enhanced spin-dependent charge number fluctuation led by fast tunneling between QDR and the electron reservoir on the right side of QDR. (e) Schematic illustration for each marker in (d) that depicts the energy levels of each dot, capacitive coupling between ST0 qubit and QDR, and the tunneling between QDR and the electron reservoir.

Electronic Measurement of Semiconductor Quantum Dot Devices

This page contains detailed information about the electronic measurement of semiconductor quantum dot devices. The project consists of three major works: (1) Bayesian estimation and fidelity optimization, (2) measurement of capacitive coupling between Singlet-Triplet qubits, and (3) Spin-Electric Coupling of Singlet-Triplet Qubits.

Work 1. Bayesian Estimation and Fidelity Optimization

In this work, we developed an energy-selective tunneling readout-based Hamiltonian parameter estimation for a two-electron spin qubit within a GaAs quantum dot array. Our achievements include:

  1. Real-Time Bayesian Estimation: We successfully implemented real-time Bayesian estimation techniques.
  2. Enhanced Single-Qubit Gate Fidelity: We significantly improved single-qubit gate fidelity through Bayesian-based active-feedback methods.
  3. Validation through Benchmarking: We confirmed the enhanced single-qubit gate fidelity through rigorous validation methods, including Randomized Benchmarking (RB) and Gate-Set Tomography (GST).

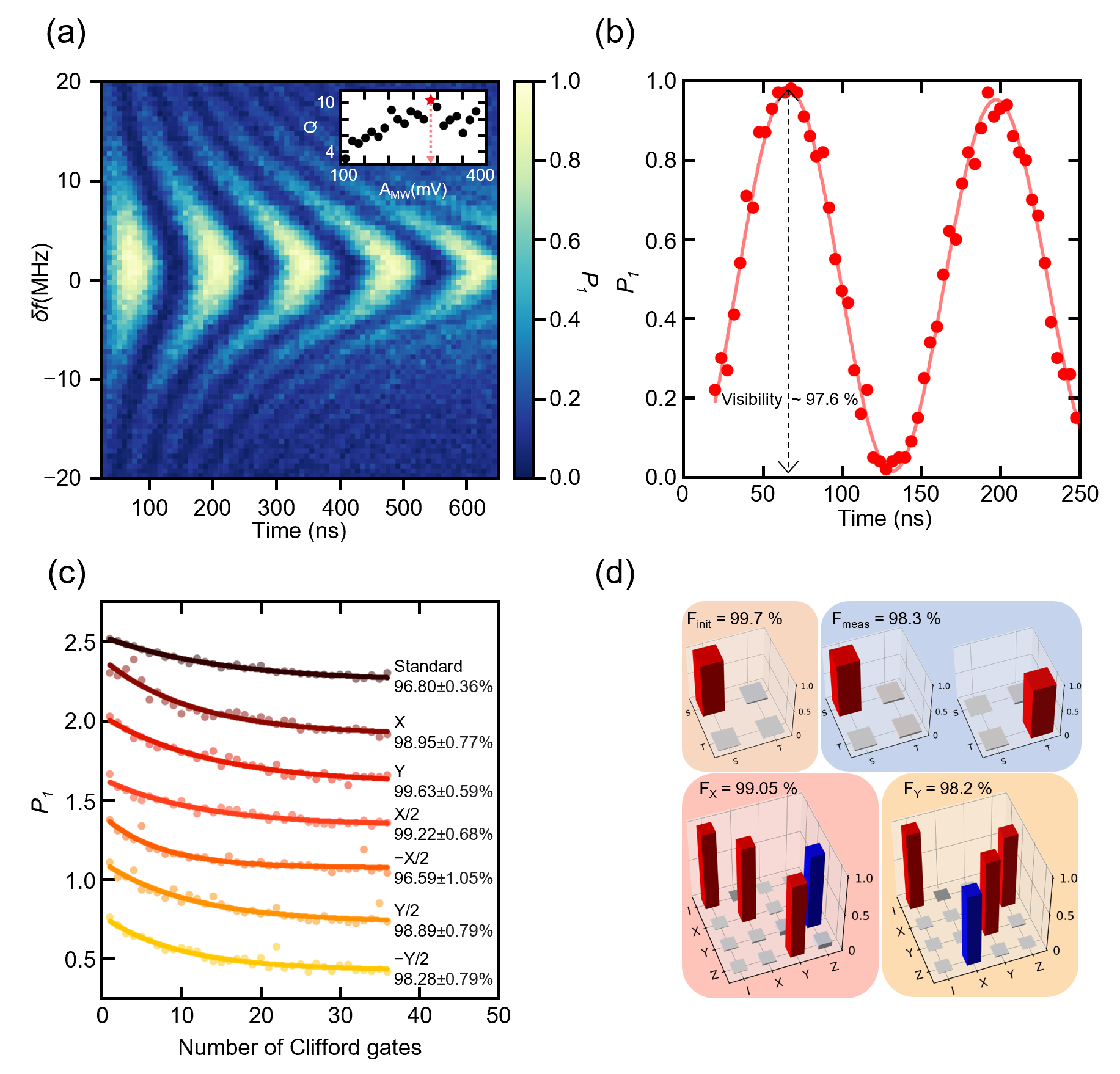
To elaborate further, our results showcased a 40-fold increase in coherence time without resorting to dynamic nuclear polarization. We demonstrated active frequency feedback with exceptional visibility and fidelity, achieving quantum oscillation visibility, single-shot measurement fidelity, and gate fidelity levels of 97.7%, 99%, and 99.6%, respectively. These achievements collectively represent substantial advancements in the capabilities of GaAs-based spin qubits. For detailed insights and representative results of this project, please refer to Figure 1, and you can find details at Phys. Rev. Lett. 129, 040501.

Work 2. Measurement of Superlinear tendency of Capacitive Coupling between Singlet-Triplet Qubits

One of the trammels that hamper singlet-triplet qubits to be used in scaling up is the weak interqubit coupling and its bilinearly increasing tendency. By implementing the simultaneous operation and two-qubit-coupling measurement of a pair of two-electron spin qubits, actively decoupled from quasi-static nuclear noise in a GaAs quadruple quantum dot array, we observed strong two-qubit capacitive interaction (>190 MHz), combined with detuning pulses, inducing a state-conditional frequency shift. The two-qubit capacitive interaction is beyond the bilinear regime, consistent with recent theoretical predictions. We observe a high ratio (>16) between coherence and conditional phase-flip time, which supports the possibility of generating high-fidelity and fast quantum entanglement between encoded spin qubits using a simple capacitive interaction. More information can be found at npj Quantum Information 9, 30 (2023)

Work 3. Spin-Electric Coupling of Singlet-Triplet Qubits and Noise Analysis

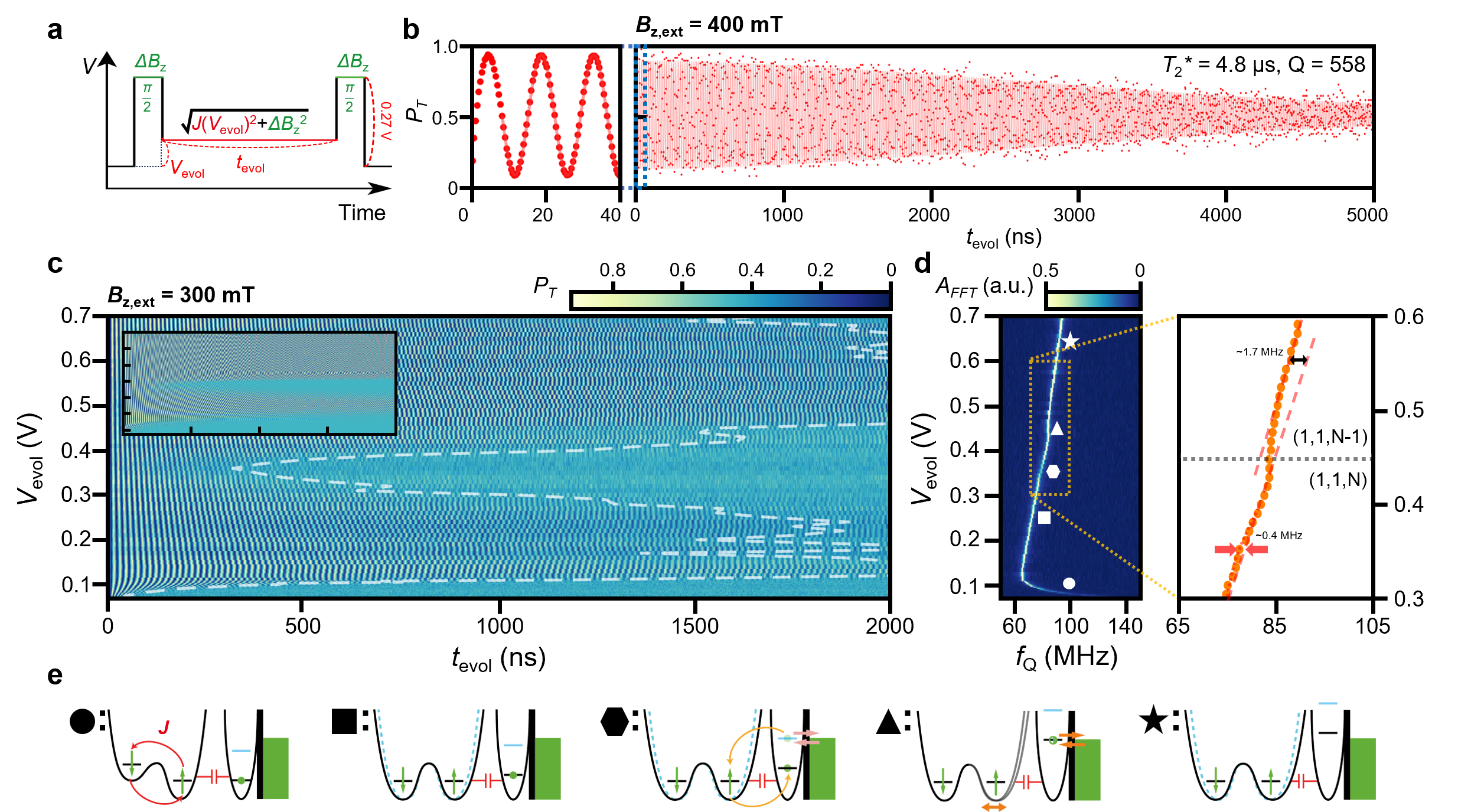
In this work, we demonstrated fast singlet-triplet qubit oscillation (~ 100 MHz) in a gate-defined double quantum dot in 28Si/SiGe with an on-chip micromagnet in the large valley-splitting regime (> 175 μeV) where proper field gradient enables the oscillation quality factor of an encoded spin qubit over 580. Notably, strong spin-electric coupling is observed as a gradient of a qubit frequency in electrical pulse detuning. We analyzed the variation of coherence time T2* as a function of confinement potential detuning and external magnetic fields where at low magnetic fields the coherence is limited by fast noise compared to data acquisition time leading to T2* < 1 μs in ergodic limit. Moreover, we showed evidence of sizable and coherent coupling of the qubit with spin states of a nearby quantum dot demonstrating that the proper amount of spin-electric coupling may enable a charge-based two-qubit gate in (1,1) charge configuration.