Figure 1 Polygon-based Genetic Algorithm for Micromagnet Shape Optimization. (a) Schematic of the geometric crossover operator. The vertices of two overlapping parent polygons are linearly interpolated (blended) to create a new offspring polygon that inherits structural features from both parents. (b) Schematic of the mutation operator. Each vertex of a polygon has a small probability of being randomly displaced within a defined boundary. The algorithm validates the new geometry to ensure the polygon remains topologically valid after mutation. (c) A representative plot showing the evolution of the population's fitness over 100 generations (epochs). The y-axis shows the Quality Factor (Q) of the best-performing individual in the population at each generation, which serves as the optimization's objective function. (d) An example of a final, optimized micromagnet geometry discovered by the genetic algorithm. The resulting non-intuitive and complex shape is evolved to generate a tailored magnetic field landscape that enhances spin qubit coherence time.
Figure 2 Comparison of Micromagnet Geometries and Resulting Qubit Coherence. (a) A conventional bar-type micromagnet geometry commonly used to generate magnetic field gradients in silicon spin qubit devices. (b) The corresponding simulated map of the qubit coherence time ($T_2*$) for the conventional design. The high-coherence "sweet spot" (bright yellow region) is confined to a very small, localized area, making it challenging to place multiple qubits with uniform high performance. (c) The complex and non-intuitive micromagnet geometry discovered and optimized by the genetic algorithm. (d) The simulated $T_2*$ map for the optimized geometry. The high-coherence sweet spot is significantly extended into a large, uniform region along the x-axis. This allows for placing multiple qubits (indicated by red dots) in locations that can simultaneously benefit from long coherence times, a critical step towards building scalable and robust multi-qubit processors.
Genetic-algorithm-based Micromagnet Shape Optimization Jan. 2025 – Jun. 2025
⌜Developed a custom genetic algorithm from scratch in Python to autonomously design complex micromagnet geometries. Implemented both mesh-based and advanced polygon-based representations, and integrated the algorithm with MuMax3 micromagnetic simulator to optimize on-chip magnetic field gradients for enhanced spin qubit coherence.⌟
The performance of spin qubits driven by Electric Dipole Spin Resonance (EDSR) is often limited by dephasing
caused by the same magnetic field gradients used to drive them.
While significant efforts in the field have focused on improving material properties or applying advanced denoising
protocols to enhance coherence,
the geometric optimization of the micromagnet itself has often been overlooked as a crucial degree of freedom.
This project aimed to overcome this fundamental trade-off by
optimizing the physical shape of an on-chip micromagnet to create an extended "sweet spot"
of high qubit coherence (T2*). As the numerical nature of the problem precluded traditional gradient-based methods,
I developed a comprehensive, gradient-free Genetic Algorithm (GA) framework from scratch in Python
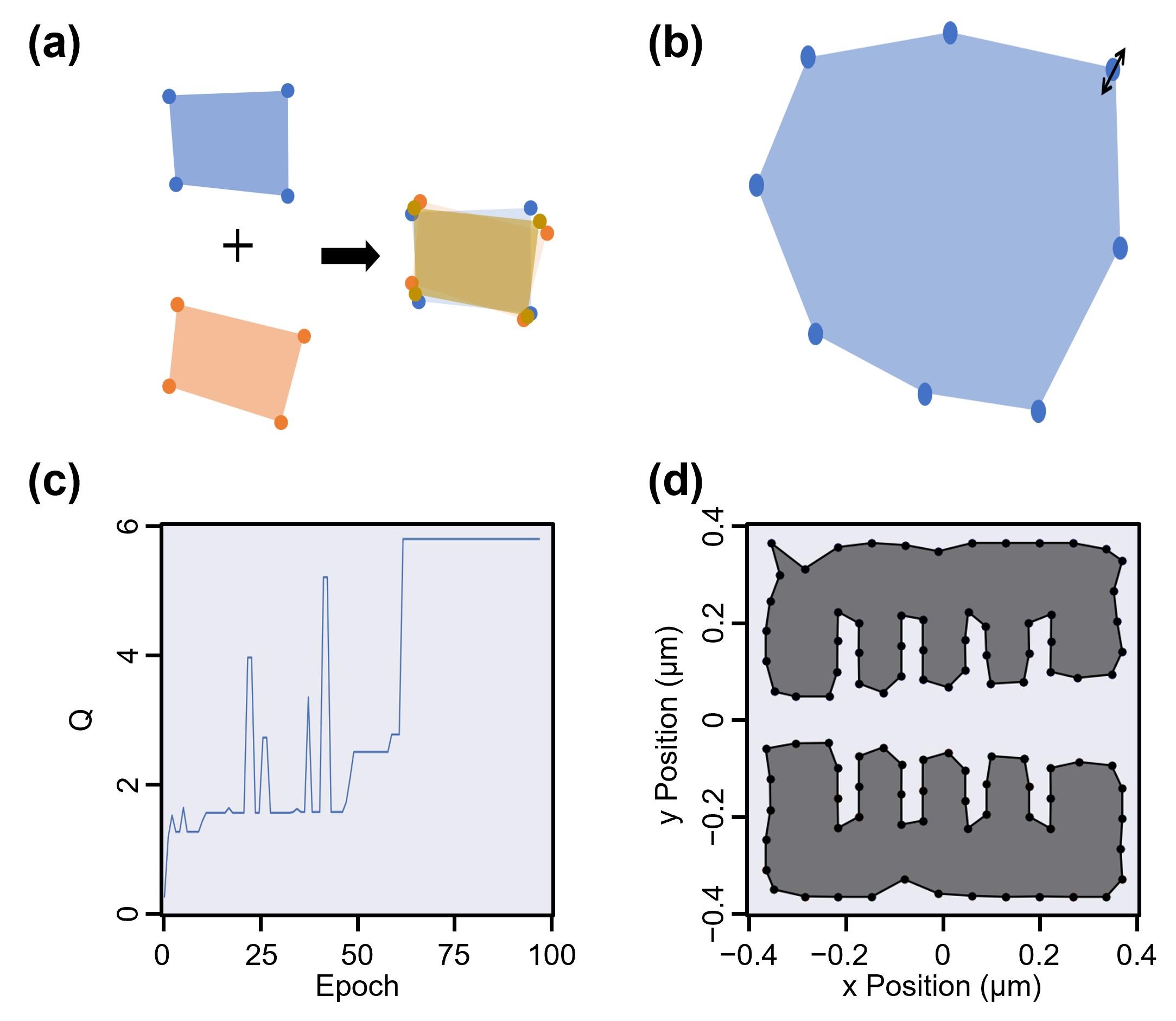
to evolve magnet shapes. This approach evolves a population of candidate micromagnet shapes, represented as
sophisticated 'MultiPolygonChrom' objects, over many generations.
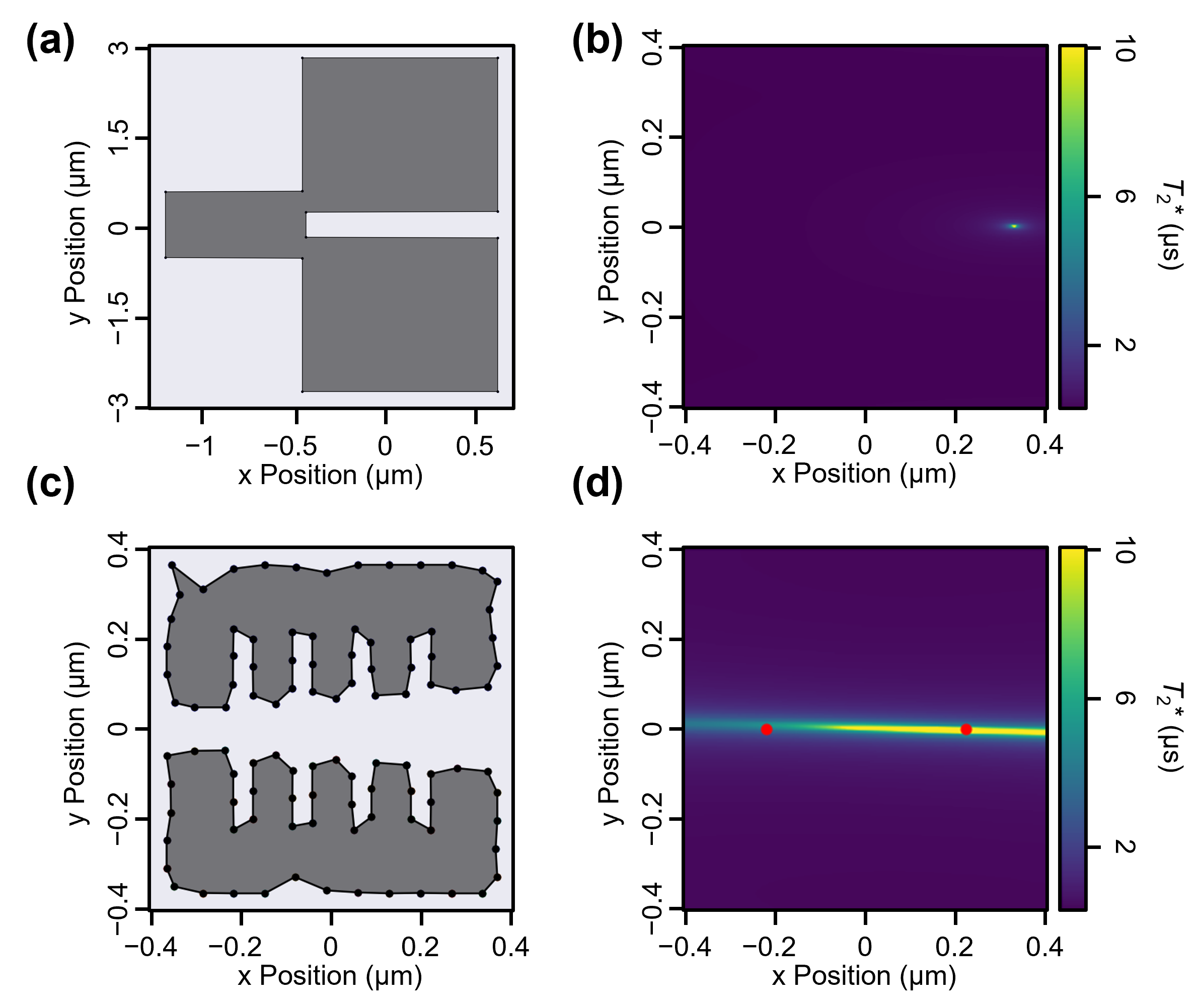
The core of the algorithm is a custom fitness function that evaluates each candidate by first calling the
MuMax3 micromagnetic simulator via a C++ backend to compute the stray magnetic field.
It then calculates local field gradients using a 3x3 stencil method to determine the qubit quality factor
($Q = T_2^* \times \delta B_{driv}$) at specific quantum dot locations.
A sophisticated penalty term was also introduced to enforce field uniformity across multiple dots,
ensuring individual qubit addressability. The evolution is driven by custom implementations of
tournament selection, geometric crossover via vertex blending,
and mutation via random vertex displacement.
Crucially, to ensure the final designs are robust against real-world manufacturing imperfections,
the framework includes an optional evaluation mode that simulates fabrication blur by applying Gaussian
offsets to the polygons and averaging the fitness over these perturbed samples.
The result is a fully automated and robust pipeline that successfully designs non-intuitive magnet geometries
for improved qubit performance.